Статья будет полезна аналитикам любых компаний, а также всем, кому интересно, как на самом деле работает аналитика и как может помочь бизнесу в проверке гипотез.
Представим ситуацию: есть FMCG-компания, которая занимается винами. Это накладывает определенные сложности на привлечение трафика: вся категория dark market ограничена в инструментах.
У компании есть сайт и регулярные email-рассылки с бонусами, акциями и предложениями. Пользователи на эти письма реагируют хорошо, посетители на сайте регулярные, чего еще желать? Но приходит новый квартал, а с ним — новые KPI и новые задачи: избавляться от бесконечных бонусов и призов.
Что будет, если использовать в письмах только органический контент? Можно в таком случае выполнить KPI? Расскажет регрессионная модель.
Что такое регрессионная модель
Это что-то похожее на уравнение, которое описывает конкретную ситуацию. Модель показывает, как меняется какой-то из показателей в динамике — зависимая переменная.
Влияют на нее внешние факторы, то есть регрессоры. Влиять они могут по-разному, и быть их может очень много. Чем больше, тем точнее обычно модель.
Если рассматривать нашу ситуацию, зависимой переменной будет наш KPI, а именно количество сессий на сайте.
Предполагай и проверяй
Каждая модель доказывает или опровергает гипотезу. В нашем случае она могла звучать как «а зачем нам эти письма с промо, они ж бесполезные», но можно ее сформулировать более точно: «упоминание бонусов в письмах незначимо влияют на посещаемость сайта».
Для этого нам необходимо оценить комплексное влияние email-стратегии на посещаемость, а не только переходы из писем с бонусами: мы считаем, что частота и содержание писем влияют и на интерес к сайту вообще, и на коэффициент удержания (retention rate), который вот так просто не измерить.
Самое ценное — данные
Построить модель просто так нельзя: это все-таки аналитика. Для любого прогноза нужны данные за прошедший период.
У нас есть следующие:
- посещаемость сайта по дням;
- даты отправки email и их содержание;
- план рассылок на квартал и их содержание;
- другие случайные источники трафика.
Мы свои взяли из Google Analytics, но можно, конечно, и руками их собрать в Excel.
В нашем массиве разрез данных идет по дням. Проанализировав его, мы выделили следующие регрессоры:
- Sessions — сессии или посещаемость сайта;
- Letter — наличие письма: 0 — нет, 1 — есть;
- Prize — упоминание бонуса или приза: 0 — нет, 1 — да;
- Prize as CTA — упоминание бонуса или приза с кнопкой призыва к действию: 0 — нет, 1 — да;
- Header — упоминание приза в теме письма: 0 — нет, 1 — да.
- Total email impact — сумма Letter + Prize + Prize as CTA. Здесь максимальное значение будет у дней, когда письмо было и с бонусом, и с призывом. Нам это нужно, поскольку наша гипотеза зависит от содержимого писем.
- Days since last letter — число дней, прошедших с прошлого письма. Попробуем включить этот фактор, чтобы узнать, есть ли связь с частотой рассылок.
Для точности модели убираем из показателя sessions факторы, которые влияли на трафик, например, размещение ссылки на сайт в соцсетях или промо, которые не анонсировались в email.
Чем пользоваться
Есть много разных программ. Наша модель достаточно простая, поэтому ради такой задачи покупать доступ к, например, BigQuery смысла нет. Мы выбрали gretl — он простой, понятный и бесплатный.
Что нам стоит модель построить
Есть единый алгоритм, которого мы будем придерживаться.
- Загрузить данные в программу.
- Сделать предположение о форме модели.
- Построить модель.
- Оценить качество модели. Если что-то не удовлетворит, изменить модель и построить еще раз.
- Построить прогноз.
- Сделать вывод.
С первым проблем возникнуть не должно: просто грузим файл Excel в программу.
Модель мы будем строить по данным за прошлый год, а прогноз — на будущий квартал (мы уже знаем даты рассылки на это время).
Данные разбиты по дням, где каждая строка соответствует одному дню. Значит, наша модель относится к временным рядам (они позволяют определить изменения зависимой переменной во времени).
Мы выбираем модель ARMAX, она позволяет учитывать не только регрессоры, но и предыдущие значения самой переменной.
Выбираем, что у нас — переменная, а что — регрессоры, настройки оставляем по умолчанию (шаг 1). Запускаем построение и смотрим на результат (шаг 2).
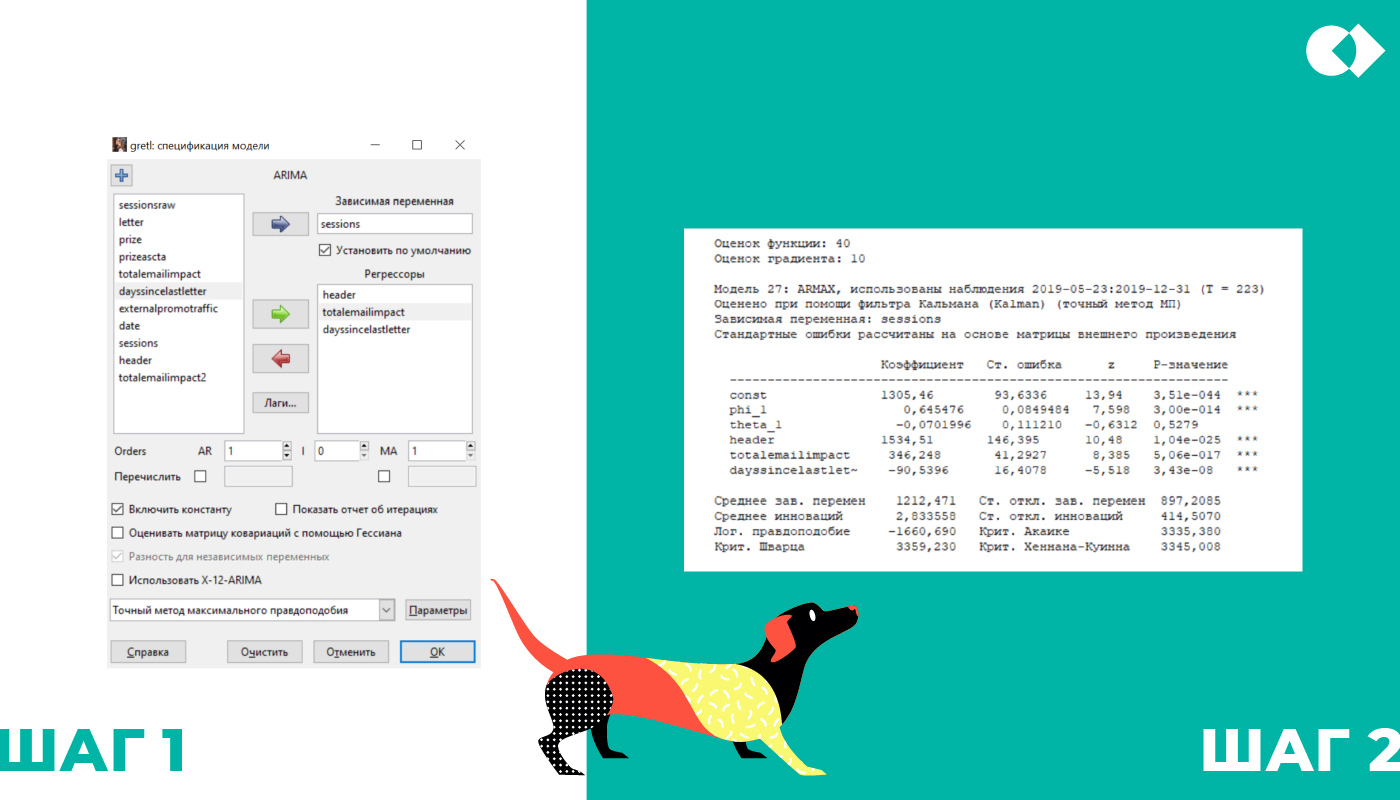
Здесь видно, что header влияет на сессии сильнее всего, total email impact — слабее, чем header, но тоже очень заметно. Сейчас не стоит проводить более детальный анализ: модель не финальная, а значит, выводы могут измениться.
Смотрим на график наблюдаемых и расчетных значений.
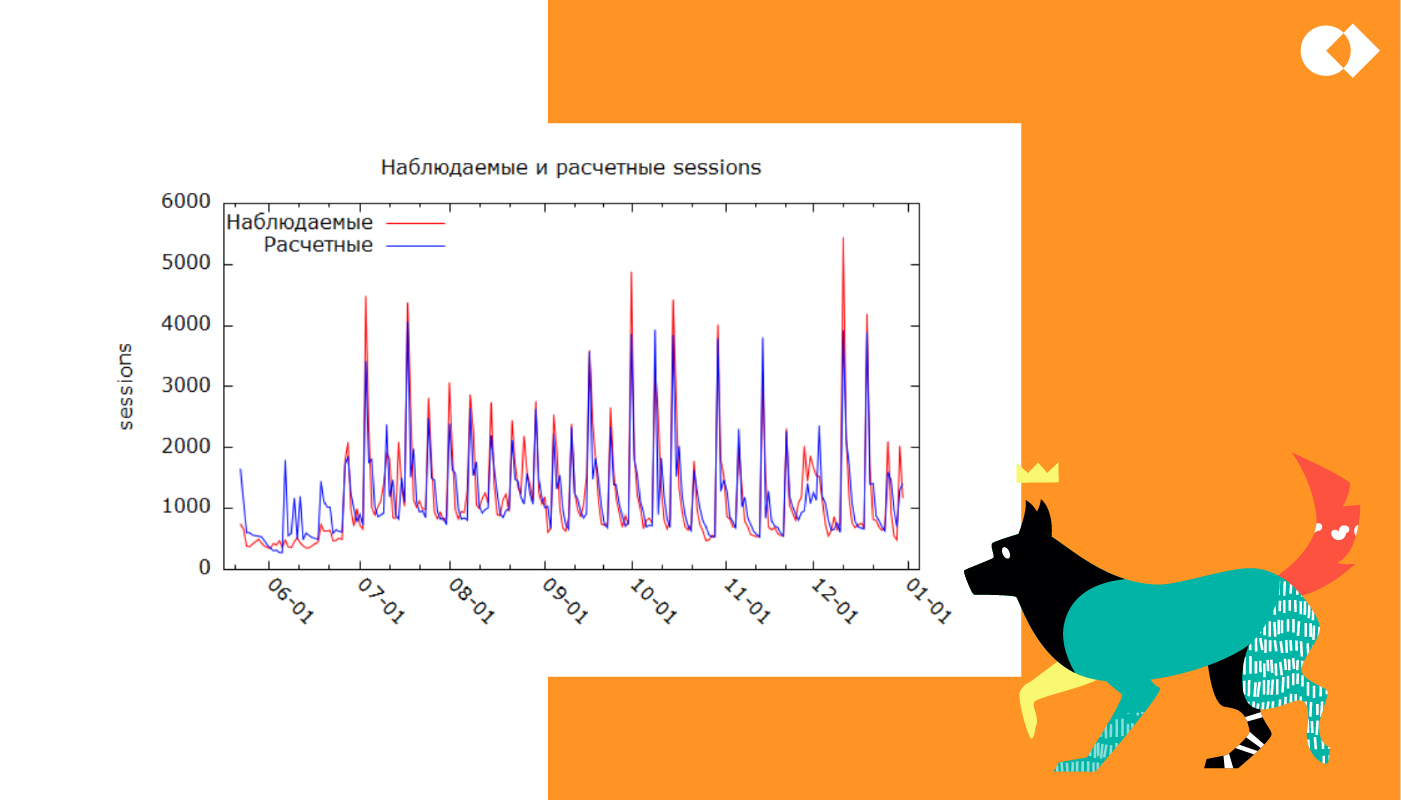
На первый взгляд, все отлично, но так это на самом деле? Сейчас узнаем!
Проводим тщательный анализ
Сравним реальные данные и модель, чтобы понять ее качество.
В p-значении (или p-value, столбик рядом с переменными) результаты должны быть ниже 0.05. Почему такая цифра? При таком уровне значимости оптимально распределяются риски неправильного вывода в результате проверки гипотезы. Если значение больше, значит, переменная для модели не значима.
Графики рассчитанных и реальных значений должны быть близки (в недостижимом идеале они совпадают) — фактический показатель не должен резко отличаться от моделируемого.
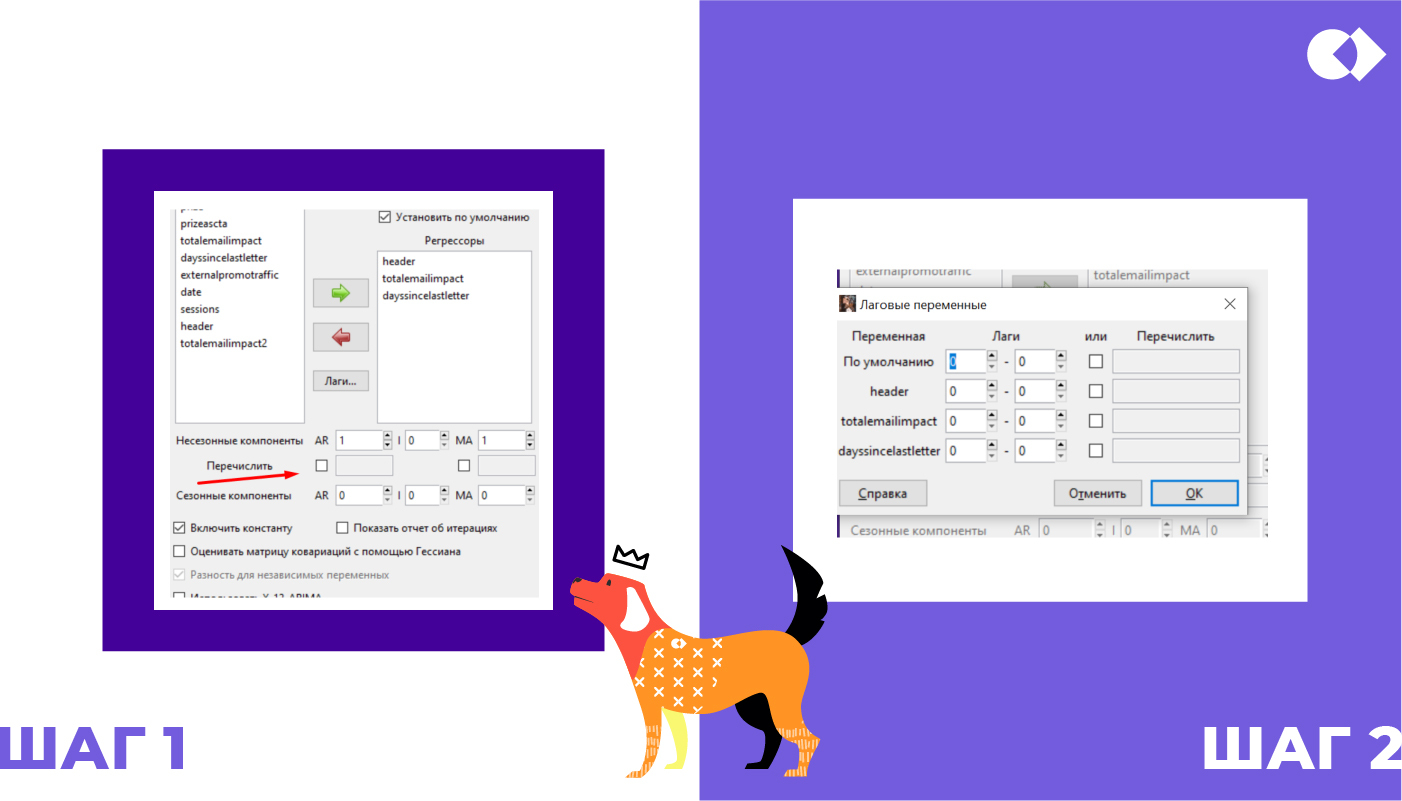
Обращаем внимание на коррелограмму остатков. Они не должны выходить за границы, рассчитанные программой. Если они выходят за рамки, смотрим, на каком лаге (они пронумерованы) и пробуем включить этот номер сначала в AR, затем MA (шаг 1).
Лаги (задержки): понятно, что чаще всего величина какого-то регрессора сегодня влияет на зависимую переменную сегодня. А что, если влияют еще и значения предыдущих дней? Например, вчерашняя рассылка влияет на сегодняшние сессии. Лаги можно «включить» (шаг 2).
Для сравнения моделей нужен еще логарифм правдоподобия. Чем меньше его значение, тем лучше.
Критерии Акаике, Шварца, Хеннана-Куинна: эта толпа поможет сделать модель еще точнее. В их формулы логарифм правдоподобия входит с минусом, поэтому чем выше значения критериев, тем лучше.
Нормальность остатков. Остатки модели — это разница между фактическим значением зависимой переменной и смоделированным. Чем меньше разница — тем лучше. Обращаем внимание на их распределение: оно должно быть нормальным.
Черная линия на рисунке — «образец» нормального распределения, на нормальность проверяем столбцы: они должны быть максимально похожи. В разных программах есть разные тесты на нормальность.
Если p-value теста >= 0.05, то остатки распределены нормально. И все отлично.
Проверяем отсутствие автокорреляции остатков с помощью теста Льюинга-Бокса. Автокорреляция — это взаимосвязь остатков модели; если модель построена правильно, ее быть не должно. Если p-value теста >= 0.05, то автокорреляции нет, и все хорошо.
Финальная модель
Наконец мы учли все критерии качества и построили финальную модель.

Расшифровываем все эти символы.
Sessions(t) — сессии в определенный день, где t — переменная времени. 809,899 — константа: это значит, что если убрать все факторы, которые влияют на посещаемость, то в среднем будет 809 посетителей в день.
Header(t) — тема письма сегодня. Если она была с указанием приза, то сегодня +1815 посетителей (в среднем).
Header(t–1) — тема письма вчера. Если она была с указанием приза, то сегодня +794 посетителей (в среднем).
Header(t–2) — тема письма позавчера. Если она была с указанием приза, то сегодня +372 посетителя (в среднем).
Влияние давности письма выразилось в переменных header(t…), а вот days_since_last_letter оказалась незначимой.
Total_email_impact(t) — вклад «внутреннего содержимого письма» сегодня. Значение этой переменной (0,1,2) умножаем на 566, чтобы узнать, сколько в среднем сегодня посетителей получим за счет содержимого.
Total_email_impact(t–1) — тот же вклад вчерашнего письма. Значение этой переменной показывает, сколько в среднем сегодня посетителей получим за счет содержимого вчерашнего письма.
Phi1 на скрине или sessions(t–1) отражает, как значение вчерашней посещаемости влияет на сегодняшнюю. Кажется, что сильно, так что у нас должна постоянно расти посещаемость, но дни без писем компенсируют этот эффект.
Theta 1, theta 11 — коэффициенты скользящего среднего. Эти коэффициенты нужны были, чтобы модель прошла по параметрам качества.
На модели видно, что на посещаемость сайта сильно влияет отправка писем с бонусами, которые упоминаются в теме или теле письма. Есть влияние показателей и за предыдущие дни, так как влияние рассылок не моментальное (обычно открывают и читают 1–2 дня).
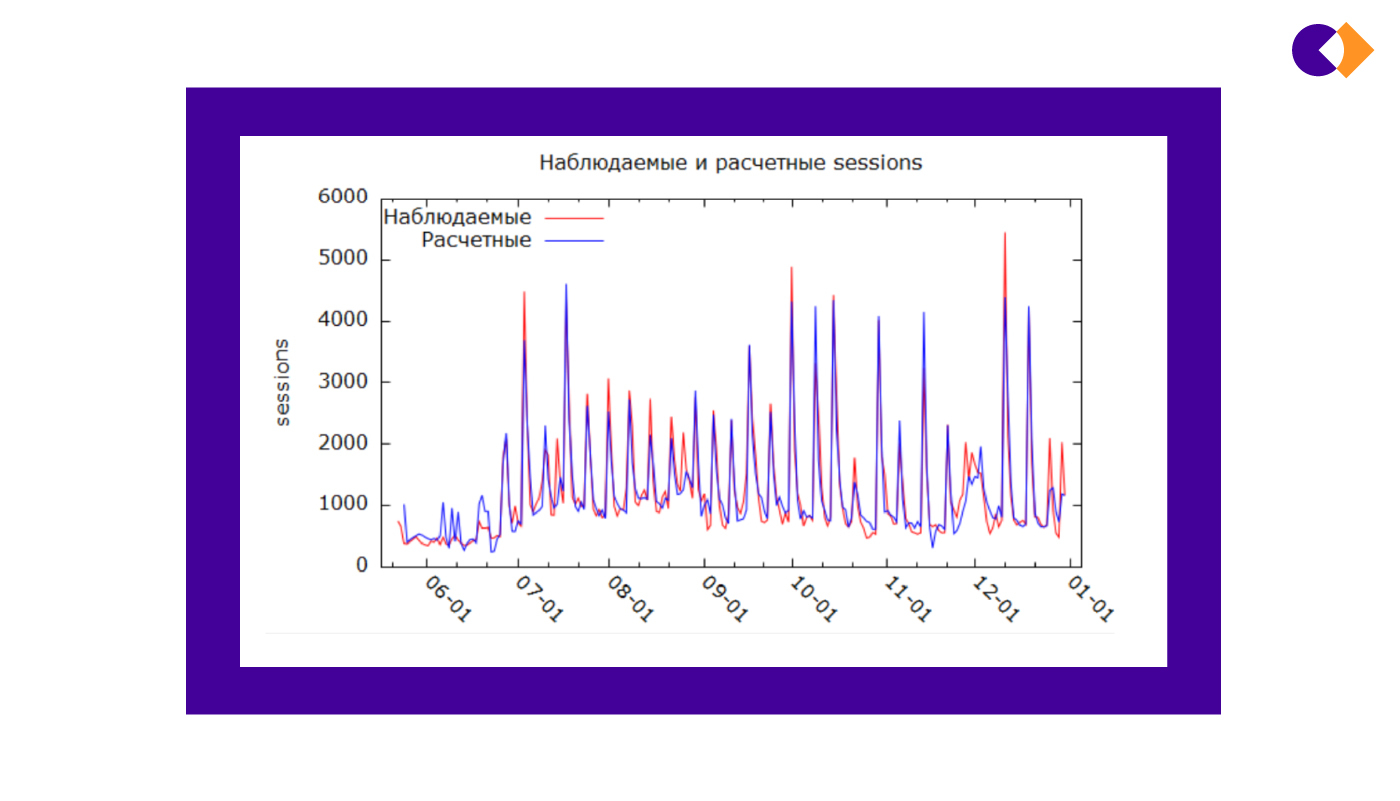
Конечно, в модели есть расхождения — они есть и в сложных научных моделях. Наша же цель заключается в том, чтобы подсчитать примерный KPI и оценить креатив в письмах, а это не очень «математическая величина».
Пришло время заглянуть в будущее
Строим прогноз. Рассылки планируются регулярные, с похожим содержанием, так что график выглядит циклично. Серая область показывает тот предел, в котором будет лежать фактическое значение посещаемости. Несмотря на сильный разброс, это все равно поможет нам сделать вывод.
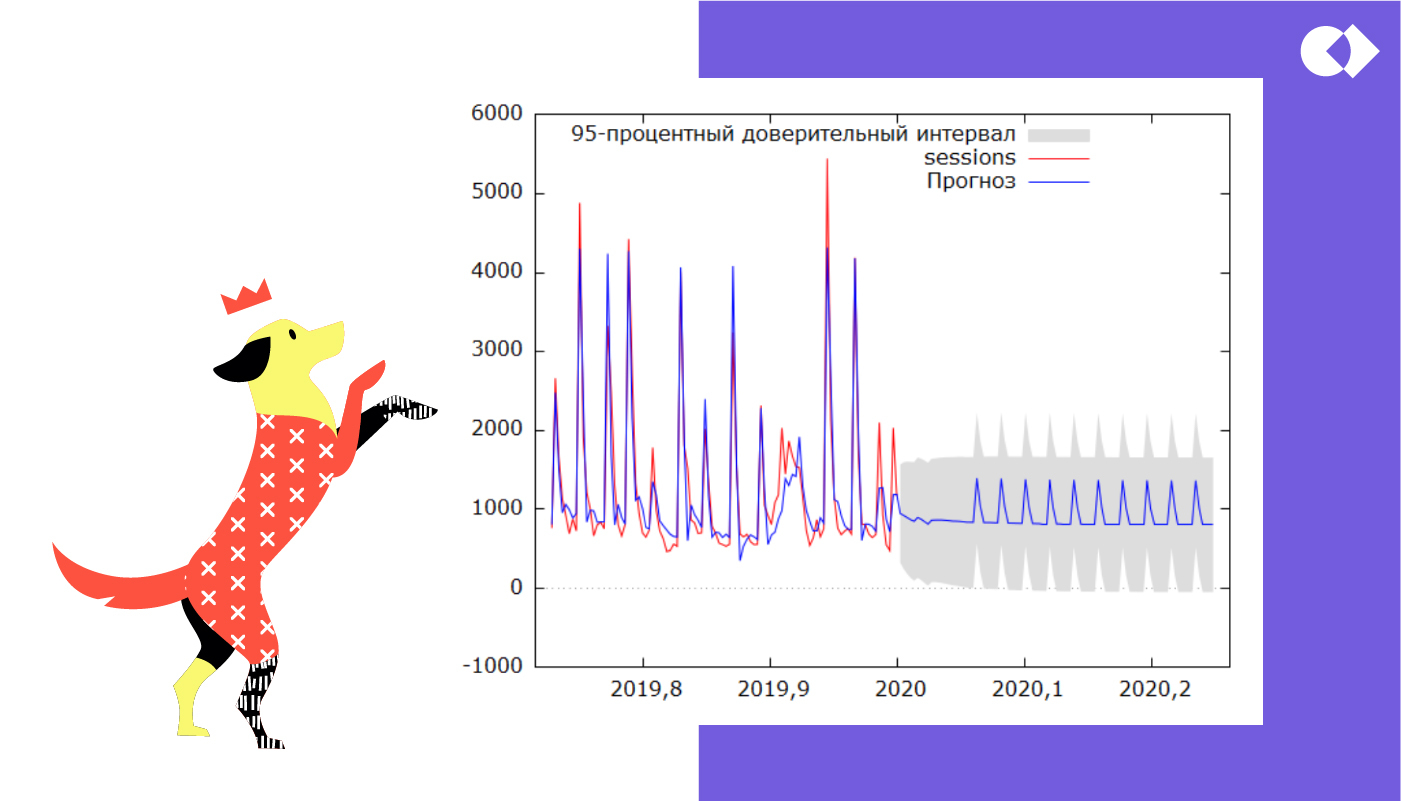
Существуют разные показатели качества прогнозов: MPE, MAPE и другие, но они имеют смысл только если прогнозов несколько. Мы здесь приводим достаточно простой пример, так что ими пользоваться не будем.
В нашей гипотезе нужно было выяснить, выполним ли мы KPI по посещениям за квартал, так что складываем все значения по дням. Увы, результат неутешительный: с такими данными мы выполним только 65% от наших планов.
Делаем выводы
Регрессионная модель показала, что наше предположение оказалось неверным и отказываться от промо-писем пока рановато. Тому есть веские доказательства — еще и на графиках. Грустно, зато правдиво. Придется разрабатывать другую стратегию. Но это уже другая история!
Как достичь максимума
- Сформулировать гипотезу. Любая модель строится, чтобы ее подтвердить или отклонить, так что с этого начинается любой прогноз.
- Собрать данные. Без точных данных за длительный период модель получится не соответствующей действительности и будет содержать много ошибок.
- Построить модель. Загружаем данные в выбранную программу, определяем форму модели и строим.
- Оцениваем качество модели. Первая построенная модель редко соответствует всем критериям качества. Нужно обратить на такие показатели, как p-значение, коррелограмма остатков, логарифм правдоподобия и информационные критерии.
- Построить прогноз. Если качество модели нас удовлетворит, то по ней уже можно сделать прогноз. Для простых прогнозов можно не использовать критерии качества.
- Делаем вывод. Проанализировав прогноз и саму модель, мы сможем понять, верна ли наша гипотеза.
Первоисточник: rb.ru
Другие статьи:
Неактивные подписчики в рассылке: откуда они
берутся и что делать



